box plot for non normal distribution If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data. This universal stainless steel smoker box is made with 25% thicker metal than most standard models out there today. The extra thickness means that the metal can withstand seriously high heat without melting, warping, or wearing thin.
0 · skewed to the right boxplot
1 · positively skewed distribution box plot
2 · positively skewed box plots
3 · positive skew vs negative boxplot
4 · how to interpret boxplot results
5 · boxplot skewed to the left
6 · box and whiskers chart explained
7 · 25th percentile on a boxplot
Multi-chapter guide to M-Code describing: what is M-Code for CNC machining, M Code vs. G Code, Benefts of M Code, Commands, FAQ's, reference list, and more.
If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data.
The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank . The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in .
You require an assumed distribution in order to be able to classify something as lying outside the range of expected values. Even if you do assume a normal distribution, declaring data points .
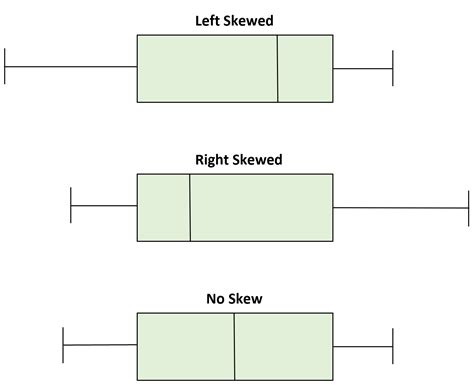
Is it the best way to summarize a non-normal distribution? Probably not. Below is a skewed distribution shown as a histogram and a boxplot. You can see the median value of the .Departures from a normal distribution alter the appearance of the box plot. To illustrate this, we show frequency distributions and descriptive statistics in Table 2, histograms in Figure 3, and .Like reliability analysis, you can use a non-normal distribution to calculate process capability, or alter-natively, you can try to transform your data to follow a normal distribution using either the .
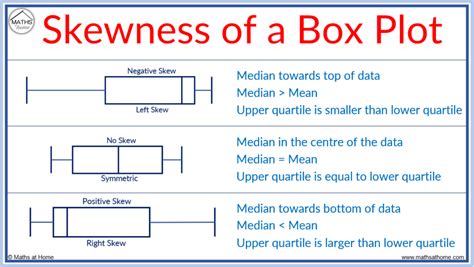
Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum .One simple method is with a QQ plot. To do this, use 'qqplot (X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a straight line, the sample is not normal. For example if X = .Create a box plot for the data from each variable and decide, based on that box plot, whether the distribution of values is normal, skewed to the left, or skewed to the right, and estimate the value of the mean in relation to the median.
If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data. The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in the interval $[101,428; 101,436]$.You require an assumed distribution in order to be able to classify something as lying outside the range of expected values. Even if you do assume a normal distribution, declaring data points as outliers is a fraught business. Is it the best way to summarize a non-normal distribution? Probably not. Below is a skewed distribution shown as a histogram and a boxplot. You can see the median value of the boxplot is accurate and the quartile markers (the edges of the 'box') show the skew. The outliers also indicate a skew.
A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.Departures from a normal distribution alter the appearance of the box plot. To illustrate this, we show frequency distributions and descriptive statistics in Table 2, histograms in Figure 3, and box plots in Figure 4. We are going to look at four examples of non-normal distributions: (A) skewed, (B) peaked, (C) flat, and (D) bimodal.
skewed to the right boxplot
Like reliability analysis, you can use a non-normal distribution to calculate process capability, or alter-natively, you can try to transform your data to follow a normal distribution using either the Box-Cox or Johnson transformation. When you transform your data, you modify the original data using a function of a variable. Functions Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score.One simple method is with a QQ plot. To do this, use 'qqplot (X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a straight line, the sample is not normal. For example if X = exprnd(3,1000,1) as above, the sample is non-normal and the qqplot is very non-linear:Create a box plot for the data from each variable and decide, based on that box plot, whether the distribution of values is normal, skewed to the left, or skewed to the right, and estimate the value of the mean in relation to the median.
sheet metal paneling
If I plot some data in function of a categorical variable in R, I get the standard boxplot. However, the boxplot displays non-parametric statistics (quantiles) that don't seem appropriate for normally distributed data. The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in the interval $[101,428; 101,436]$.
You require an assumed distribution in order to be able to classify something as lying outside the range of expected values. Even if you do assume a normal distribution, declaring data points as outliers is a fraught business.
sheet metal oakland
positively skewed distribution box plot
Is it the best way to summarize a non-normal distribution? Probably not. Below is a skewed distribution shown as a histogram and a boxplot. You can see the median value of the boxplot is accurate and the quartile markers (the edges of the 'box') show the skew. The outliers also indicate a skew.A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.Departures from a normal distribution alter the appearance of the box plot. To illustrate this, we show frequency distributions and descriptive statistics in Table 2, histograms in Figure 3, and box plots in Figure 4. We are going to look at four examples of non-normal distributions: (A) skewed, (B) peaked, (C) flat, and (D) bimodal.
Like reliability analysis, you can use a non-normal distribution to calculate process capability, or alter-natively, you can try to transform your data to follow a normal distribution using either the Box-Cox or Johnson transformation. When you transform your data, you modify the original data using a function of a variable. Functions
Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score.One simple method is with a QQ plot. To do this, use 'qqplot (X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a straight line, the sample is not normal. For example if X = exprnd(3,1000,1) as above, the sample is non-normal and the qqplot is very non-linear:
positively skewed box plots

We offer an extensive selection of plastic, concrete, polymer concrete, and composite underground pull boxes and handholes in variety of sizes. Our underground pull boxes are strong and durable, with the broadest and most .
box plot for non normal distribution|box and whiskers chart explained